2019年8月のてくてくメモ
（だいたい）2019年8月の週間歩行記録
| week | from | step(s) | step(a) | dist(s) | dist(a) | dist(t) |
|---|---|---|---|---|---|---|
| 31(281) | 0729 | 76926歩 | 10989歩 | 62.11km | 8.87km | 23995km |
| 32(282) | 0805 | 113766歩 | 16252歩 | 91.68km | 13.10km | 24087km |
| 33(283) | 0812 | 78062歩 | 11151歩 | 63.58km | 9.08km | 24151km |
| 34(284) | 0819 | 74404歩 | 10629歩 | 59.22km | 8.46km | 24210km |
| 35(285) | 0826 | 40335歩 | 5762歩 | 31.96km | 4.57km | 24242km |
s: 週合計，a: 週平均，t: 2014年第12週以降の累計
2019年7月のてくてくメモ
（だいたい）2019年7月の週間歩行記録
| week | from | step(s) | step(a) | dist(s) | dist(a) | dist(t) |
|---|---|---|---|---|---|---|
| 27(277) | 0701 | 58543歩 | 8363歩 | 45.90km | 6.56km | 23772km |
| 28(278) | 0708 | 62837歩 | 8976歩 | 50.73km | 7.25km | 23822km |
| 29(279) | 0715 | 73560歩 | 10508歩 | 59.19km | 8.46km | 23882km |
| 30(280) | 0722 | 63358歩 | 9051歩 | 51.59km | 7.37km | 23933km |
| 31(281) | 0729 | 76926歩 | 10989歩 | 62.11km | 8.87km | 23995km |
s: 週合計，a: 週平均，t: 2014年第12週以降の累計
2019年6月のてくてくメモ
（だいたい）2019年6月の週間歩行記録
| week | from | step(s) | step(a) | dist(s) | dist(a) | dist(t) |
|---|---|---|---|---|---|---|
| 22(272) | 0527 | 94112歩 | 13444歩 | 77.30km | 11.04km | 23506km |
| 23(273) | 0603 | 79127歩 | 11303歩 | 65.19km | 9.31km | 23572km |
| 24(274) | 0610 | 91286歩 | 13040歩 | 74.28km | 10.61km | 23646km |
| 25(275) | 0617 | 63443歩 | 9063歩 | 51.36km | 7.34km | 23697km |
| 26(276) | 0624 | 36912歩 | 5273歩 | 28.51km | 4.07km | 23726km |
s: 週合計，a: 週平均，t: 2014年第12週以降の累計
龍と三角関数(3)
龍と三角関数(1) - まんぼう日記
龍と三角関数(2) - まんぼう日記
→ 龍と三角関数(3) - まんぼう日記
何の役に立つの？ 〜音声や音楽を三角関数で表す〜
ここまで，いろんなグラフを三角関数の重ね合わせで描けることを見てきました．応用すると，龍の字を描いて遊んだりもできるのでした．でも，こんなことできていったい何がうれしいのでしょうか．何の役に立つのでしょうか．
実は，幅広い分野でいろいろと役に立ちます．特に理工系では道具としていろんな使い道があります（ので，大学で理工系へ進むとまじめに学ぶことになるでしょう）．しかし，それらの実例を一つ一つ挙げていくときりがありませんので，ここでは一つに絞って説明したいと思います．音声や音楽を三角関数で表すっていう話です．
例えば，携帯電話．マイクで拾った音を電波にのせて伝えるために，音の波形を数値で表します．以下の図は，そのイメージです．
送信側では，まず，音を表す波形を三角関数を使って表します．のこぎり波のグラフのときと同様です．そうしたら，sin や cos の前に現れる数値のみを送信します．受信側は，受け取った数値と sin, cos を組み合わせて式を計算します．こうすることで，元の音に近い波形を作り出すことができる，というわけです．
スマフォやPCに音楽を録音しておく際も，同様です．上記のようにして求めた数値を記録しておいて，再生するときに計算して元の波形（に近い波形）を合成するのです．音声通話のときも音楽の録音のときも，波形を表す数値の数をケチると，通信データ量や記憶容量を節約できます．ただし，そうすると元の波形をちゃんと表せないので，音質は悪くなります．のこぎり波で K が小さい時みたいな状況ですね．
とまあ，こんな感じです．高校数学ではとかく計算面倒で嫌われがちな三角関数ですが，実は，すごく役に立つありがたい存在なのです．少しは仲良くしてやってもいいかなって気に...なりましたでしょうか．
蛇足: 上記の説明ですが，わかりやすくするためにいろいろごまかしてるとこがあります．大学で情報系とか進んでちゃんと勉強すると，何をどうごまかしてるか分かるでしょう．ぜひそっち方面へ進んで将来ツッコミを入れてください (^^;
龍と三角関数(2)
龍と三角関数(1) - まんぼう日記
→ 龍と三角関数(2) - まんぼう日記
龍と三角関数(3) - まんぼう日記
三角関数重ね合わせたらなんでも表せるんや
「なんでも」とはまたずいぶん大きく出ましたが，ほんまです（数学的に厳密なこと言い出すとアレなんですが...）．「龍」の場合も，式に現れる三角関数の数が増えれば増えるほど複雑な曲線が描かれてましたよね．ここではもっと簡単なグラフを例に説明してみたいと思います．
まずはこんなん．のこぎりの歯みたいにギザギザな波形なので，のこぎり波って言います．sin とか cos みたいな曲線でほんまにこんなん作れるでしょうか． 
以下の4色の曲線は，周期の異なる4種類の正弦波（sinの式で表された波）です．
これらを重ね合わせて（足し合わせて）みると...
こんなんできます．赤いグラフが4つの sin を重ね合わせたもの．青で描いた本物ののこぎり波にそれなりに近いものができてますね．式は↑の通り．
この調子で sin をどんどん重ね合わせていくと，こーなります．
K は重ね合わせる三角関数の数．その数が大きくなると赤い曲線がどんどんのこぎり波に近づいてきます．龍と三角関数(1)で出てきたフーリエ級数展開／フーリエ変換っていうのは，こういう式を計算する方法です．
もうひとつ例を示しましょう．こちらは方形波って言います．
こちらも同様に，重ね合わせる三角関数を増やしていくと，本物に近づいていくのがわかります．
こちらは cos ばかりの式になってます．
ちうわけで，三角関数重ね合わせたらなんでも表せそうって納得していただけたでしょうか．龍の字の場合は，3つの部品の曲線それぞれのx座標の変化，y座標の変化を個別に三角関数で表していた（だから式が6つあった）のでした．
龍と三角関数(3) - まんぼう日記 へつづく
龍と三角関数(1)
→ 龍と三角関数(1) - まんぼう日記
龍と三角関数(2) - まんぼう日記
龍と三角関数(3) - まんぼう日記
某所に，理工系らしいおもしろネタを書くっちうことになりまして，「何らかの図形の輪郭線をフーリエ級数で表して描く」って方向でいってみることにしました． で，「あのロゴ描く，ついでに破壊する」とか「平成→令和」とかいろいろ考えたあげく，上記の図形でやってみました．この書は，うちの研究室のK氏の作品です（ありがとうございます）．
ちうわけで，この記事はそのネタの習作のよーなもんです．
三角関数でお絵描き
「三角関数でなんか面白いことして」っちう無茶振りを受けまして，こんなん作ってみました．
三角関数なんぞ見たくもないってひともいるかもしれませんが，だいじょーぶ．計算するわけやのーて単に眺めるだけやから怖くないですよ．って，説明せえへんかったらわけわからへんですね (^^;
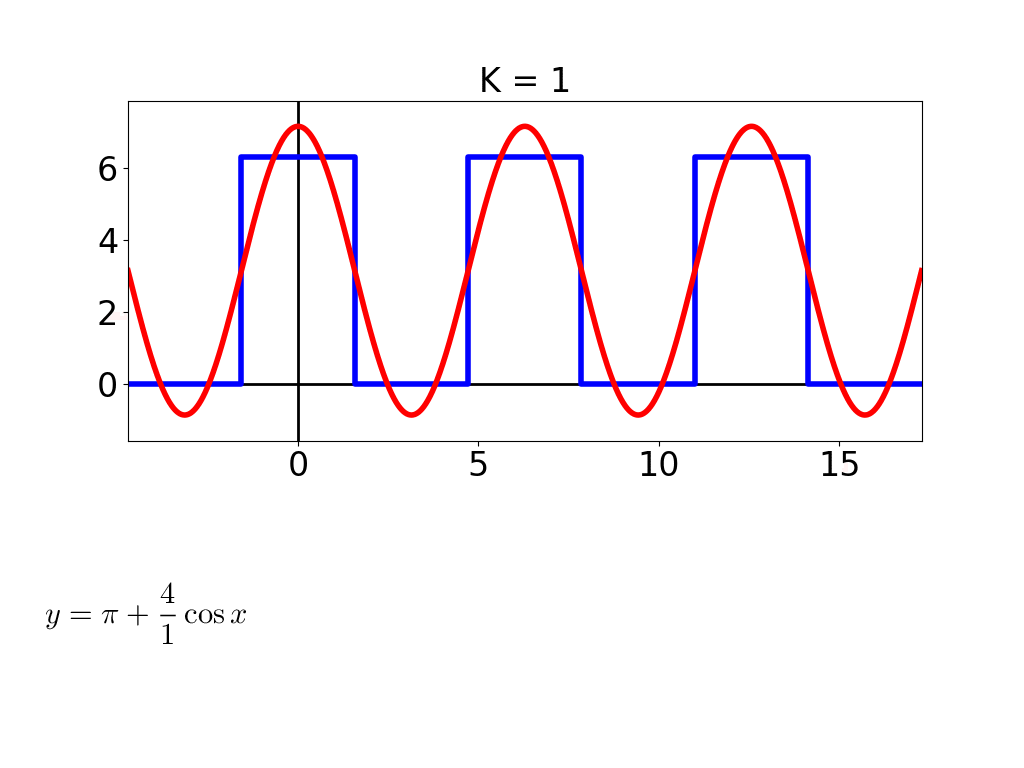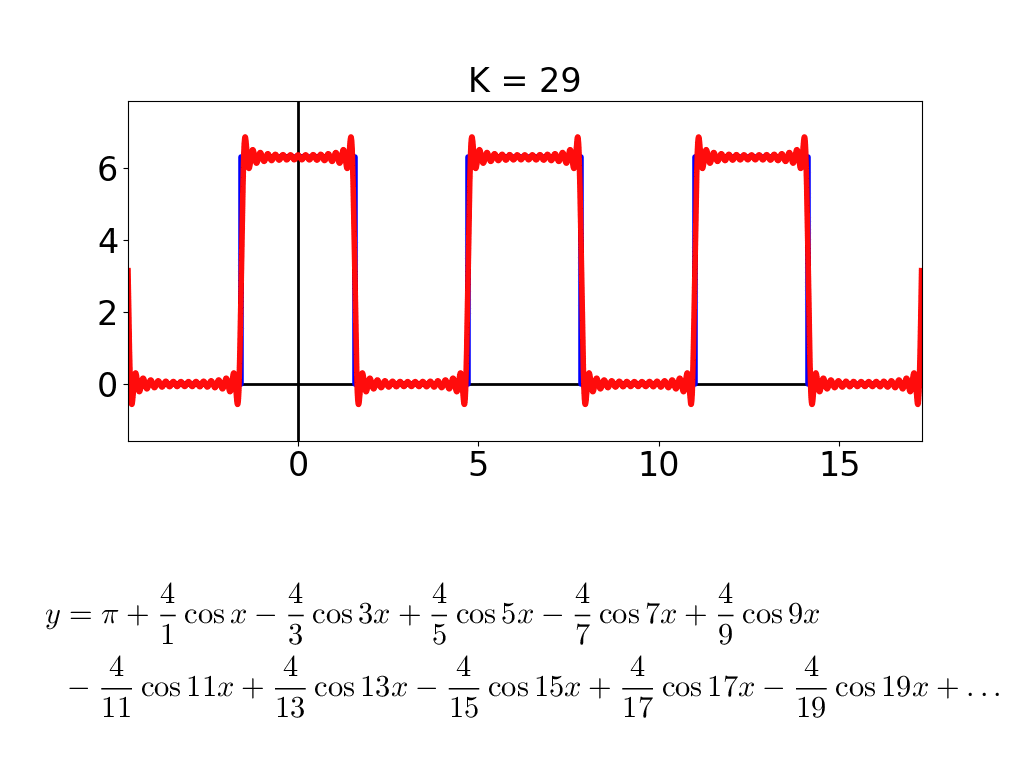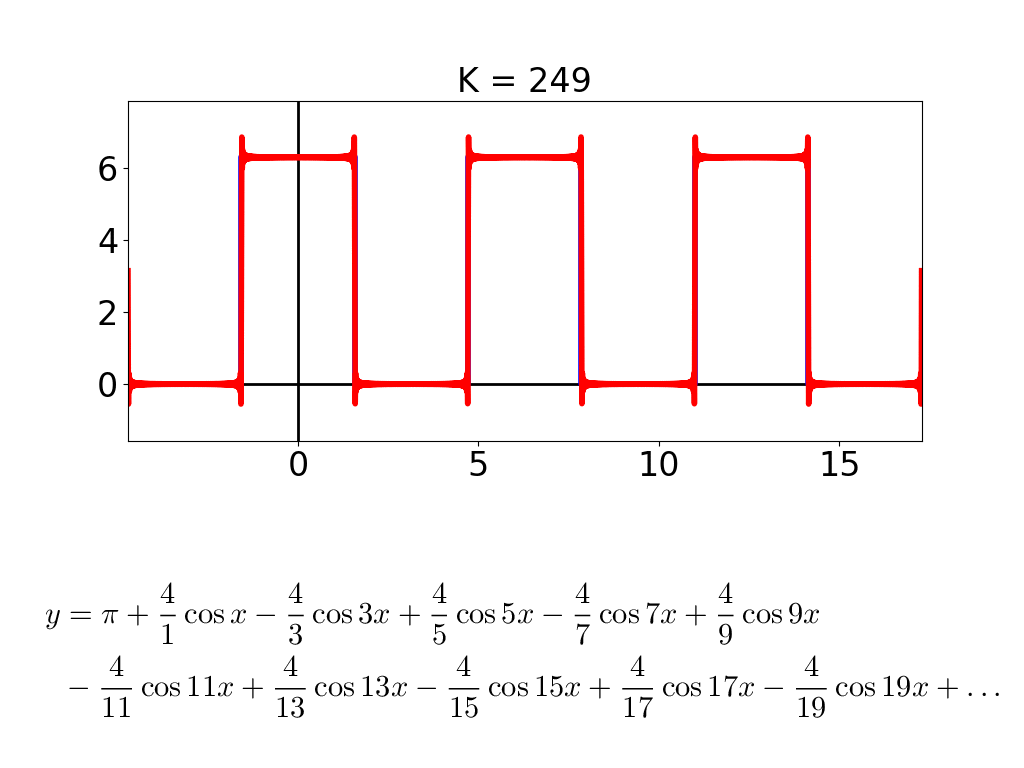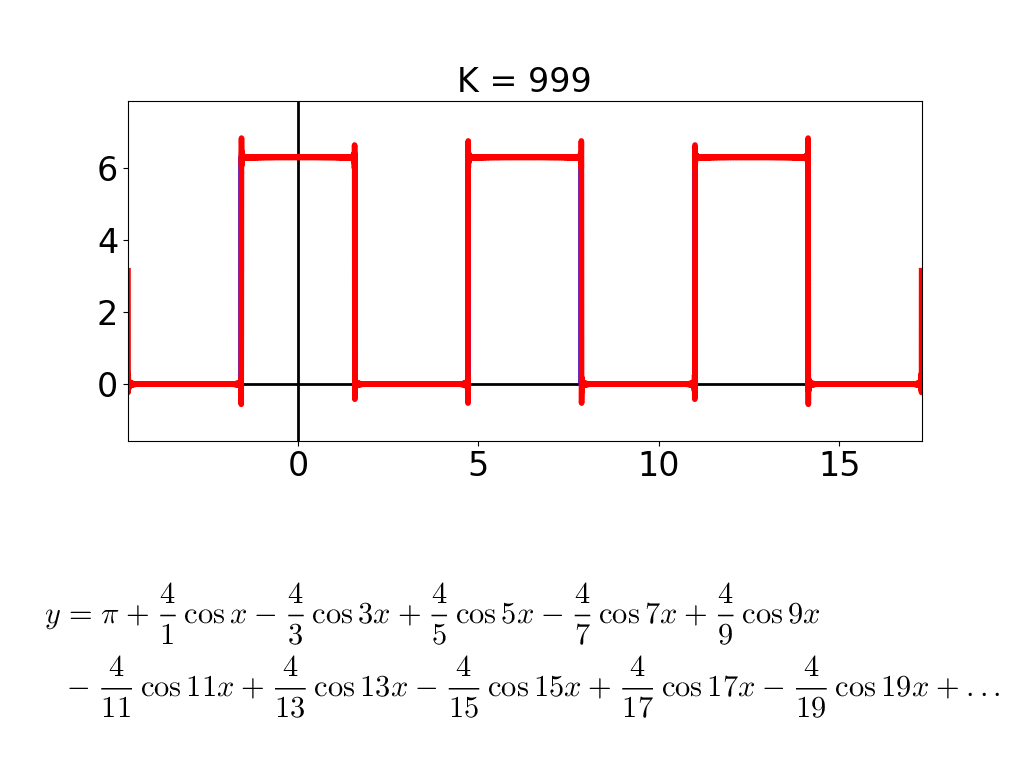
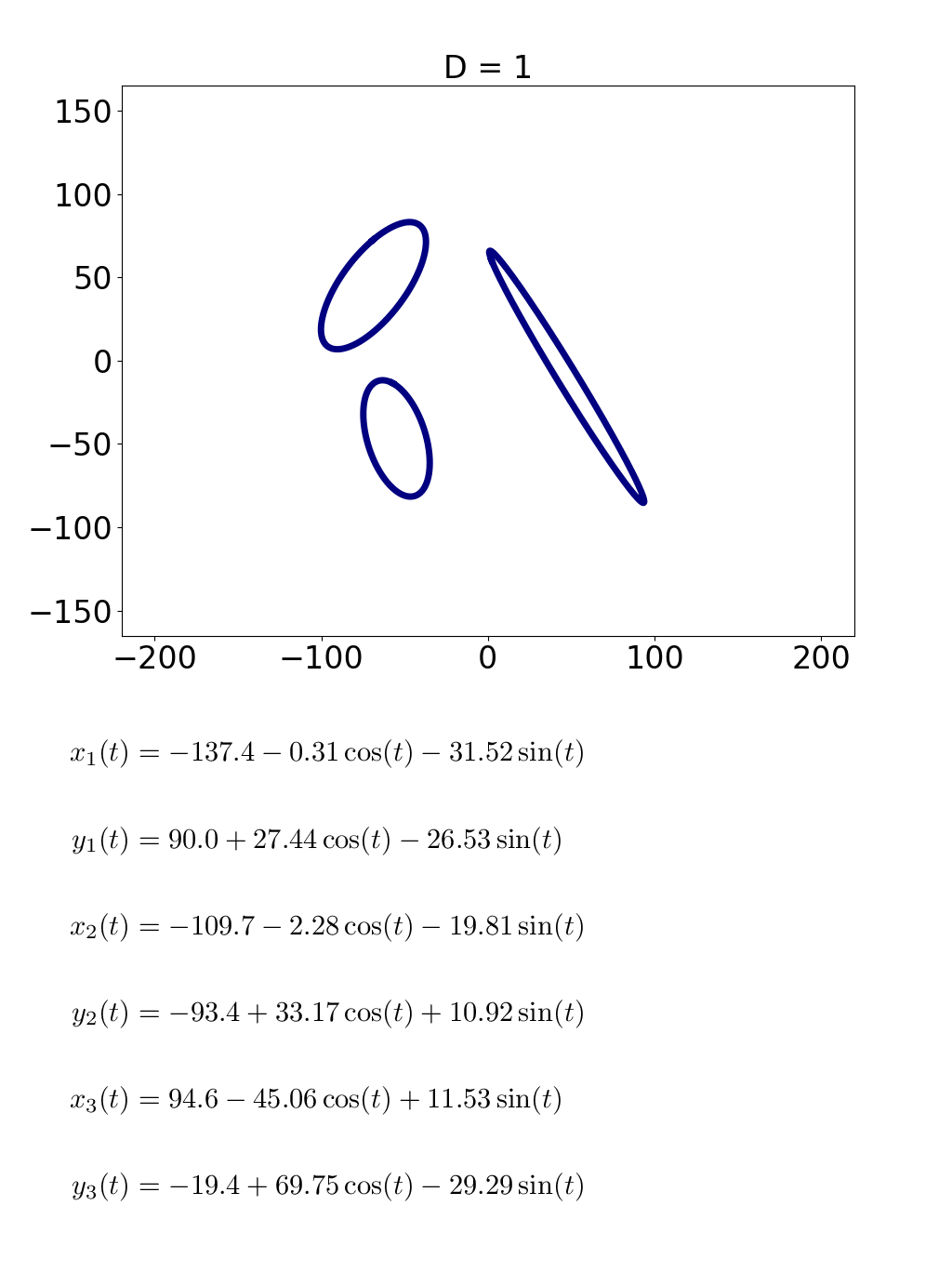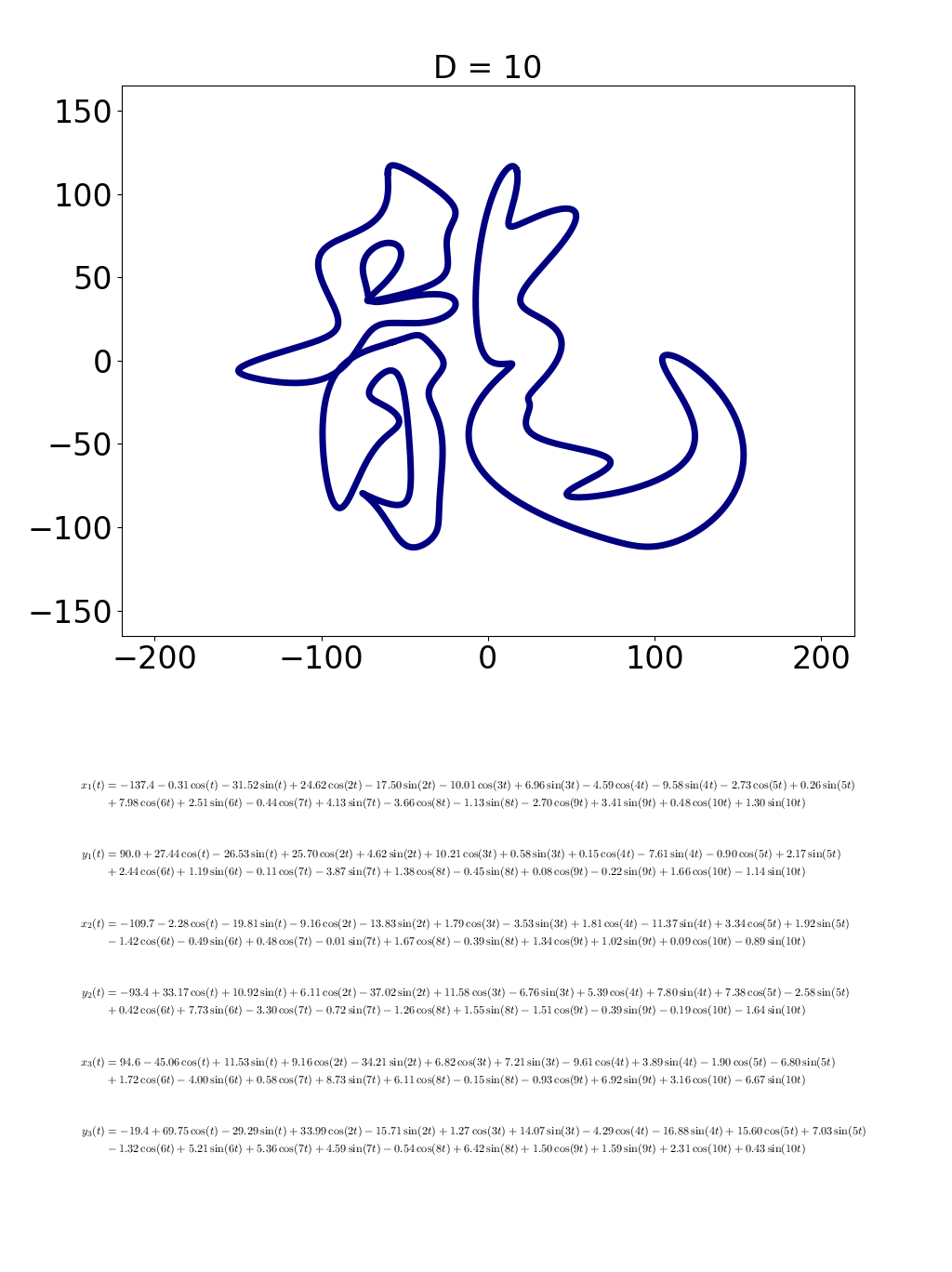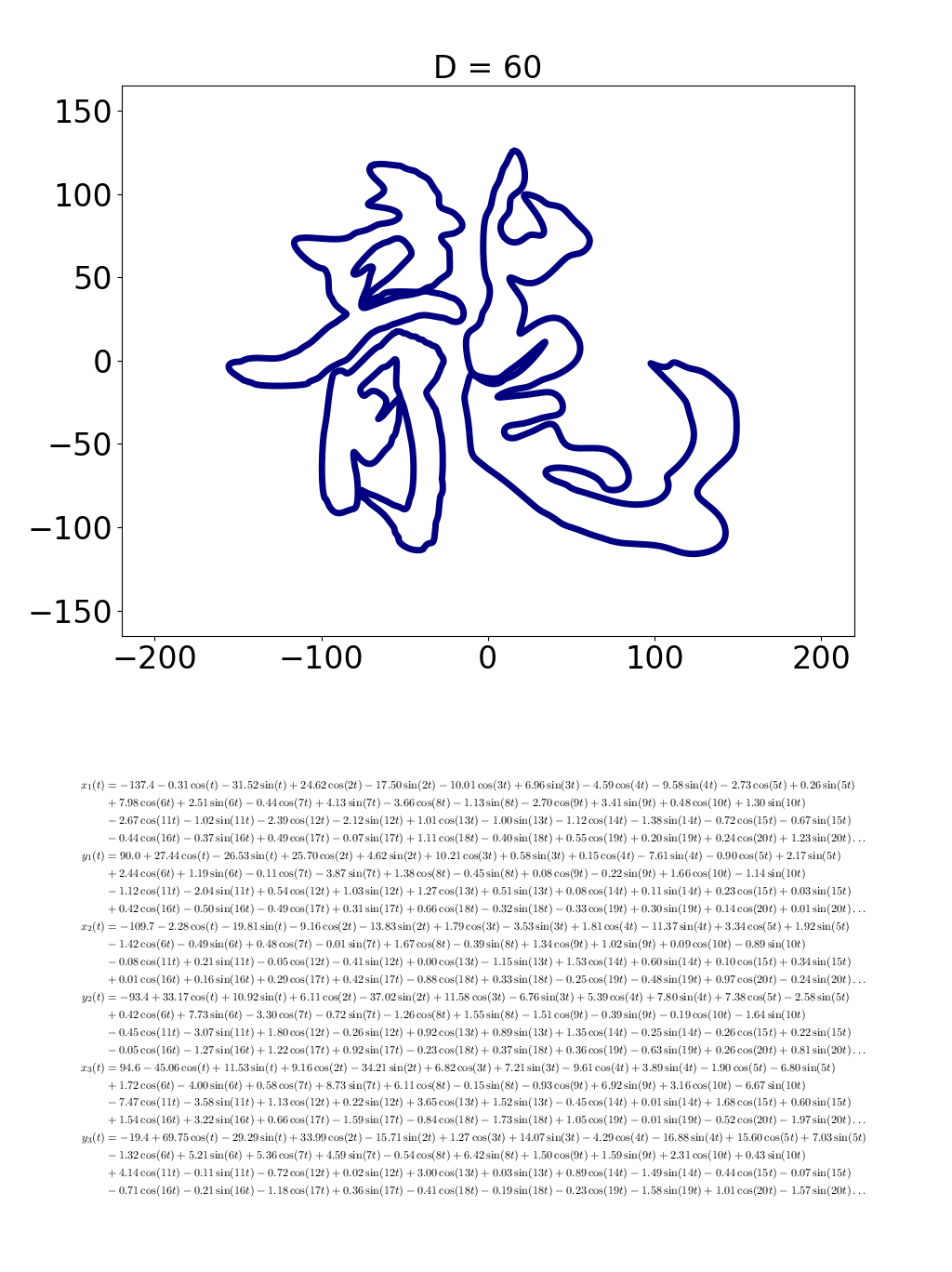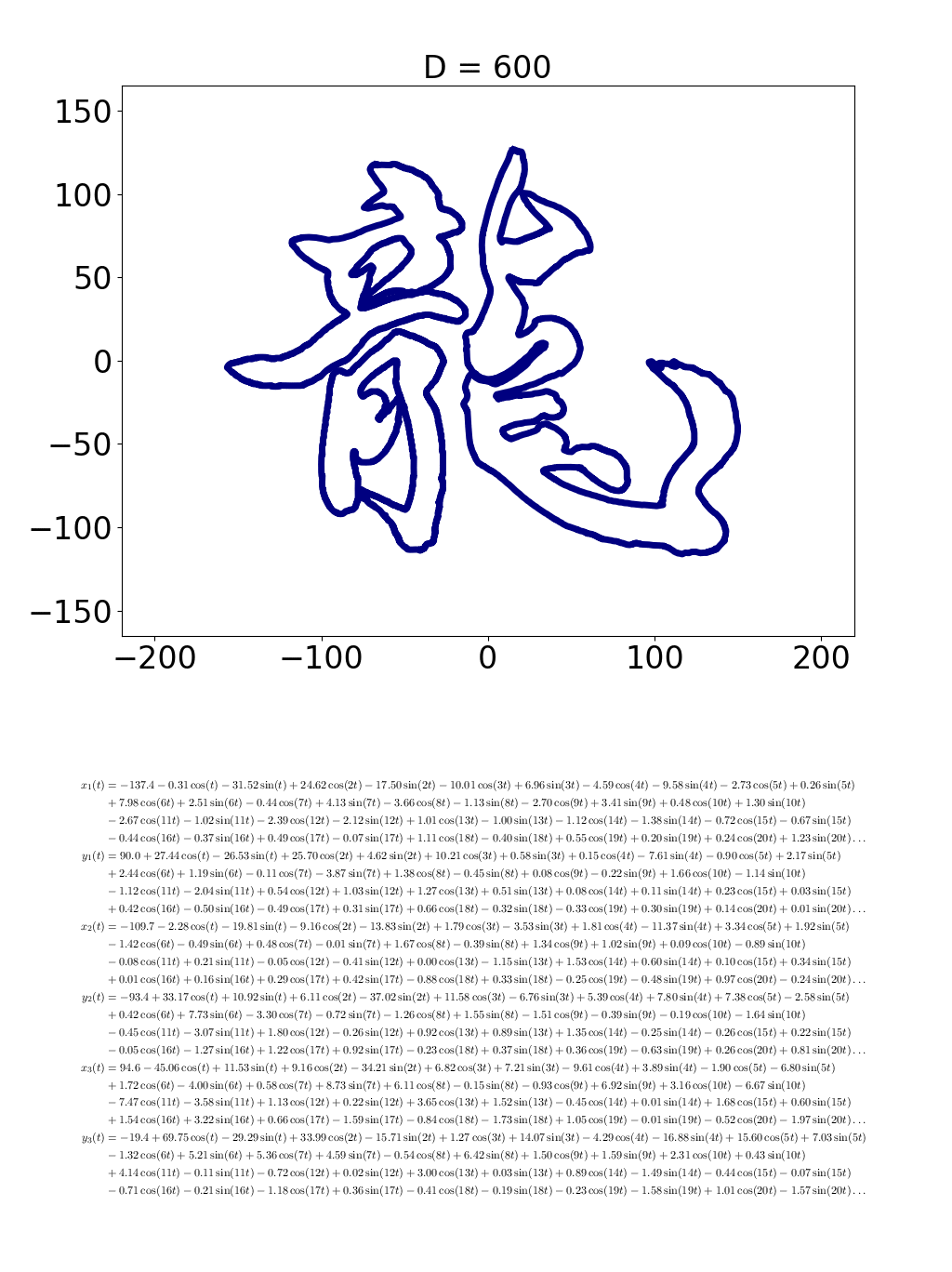
一番上のところが D = 1 からだんだん大きくなるにつれて， 「龍」の字を形作っている図形の形が複雑になってるのがわかるでしょうか． それとともに，下に出てる式もどんどん長くなってってます． 実は，これら6つの式は2つずつセット（x座標の式とy座標の式）で龍の字の3つの部品（「立」，「月」とつくりの部分）を描いてます．どの式も cos(t) とか sin(2t) みたいな三角関数ばかりでできてます．
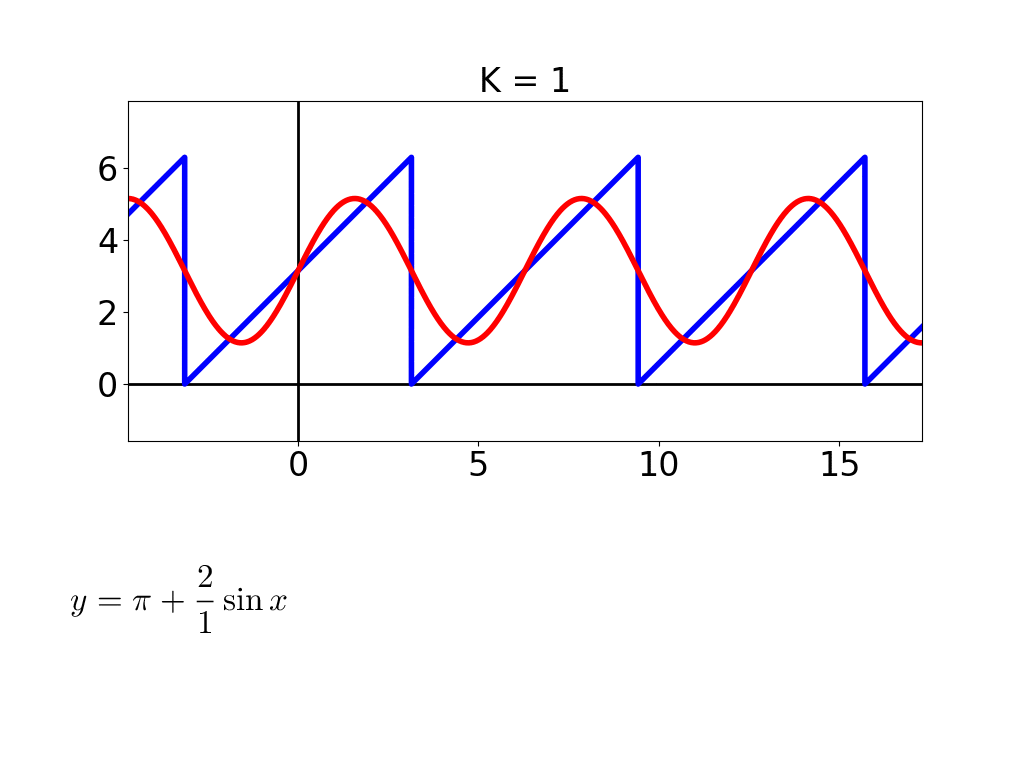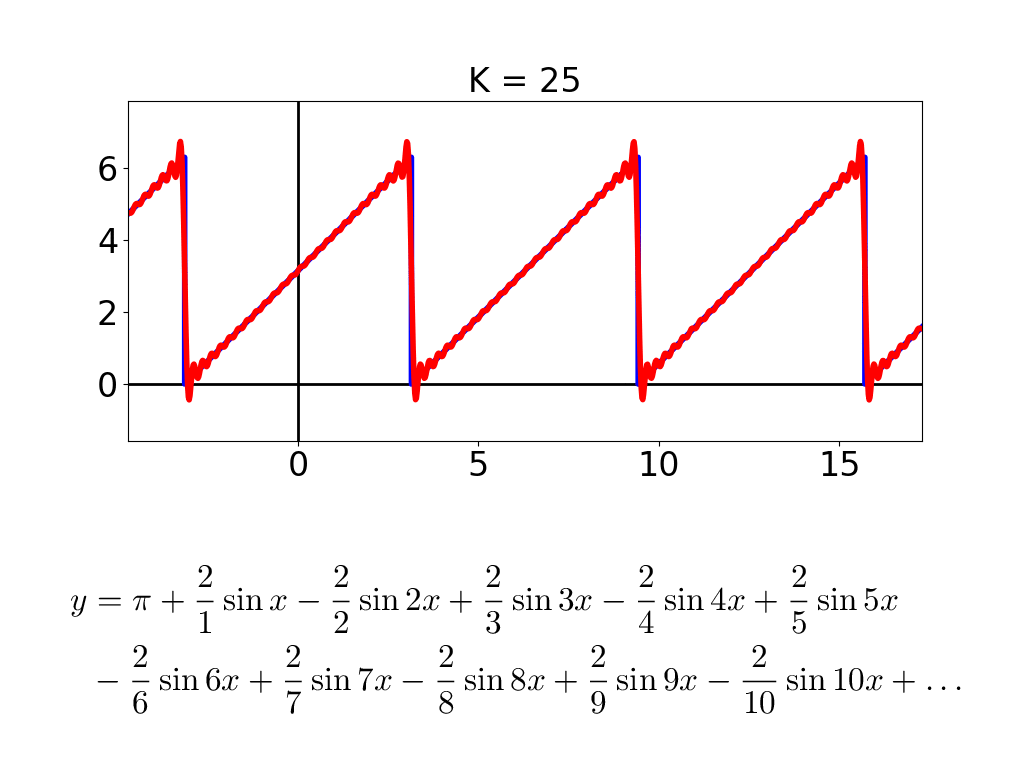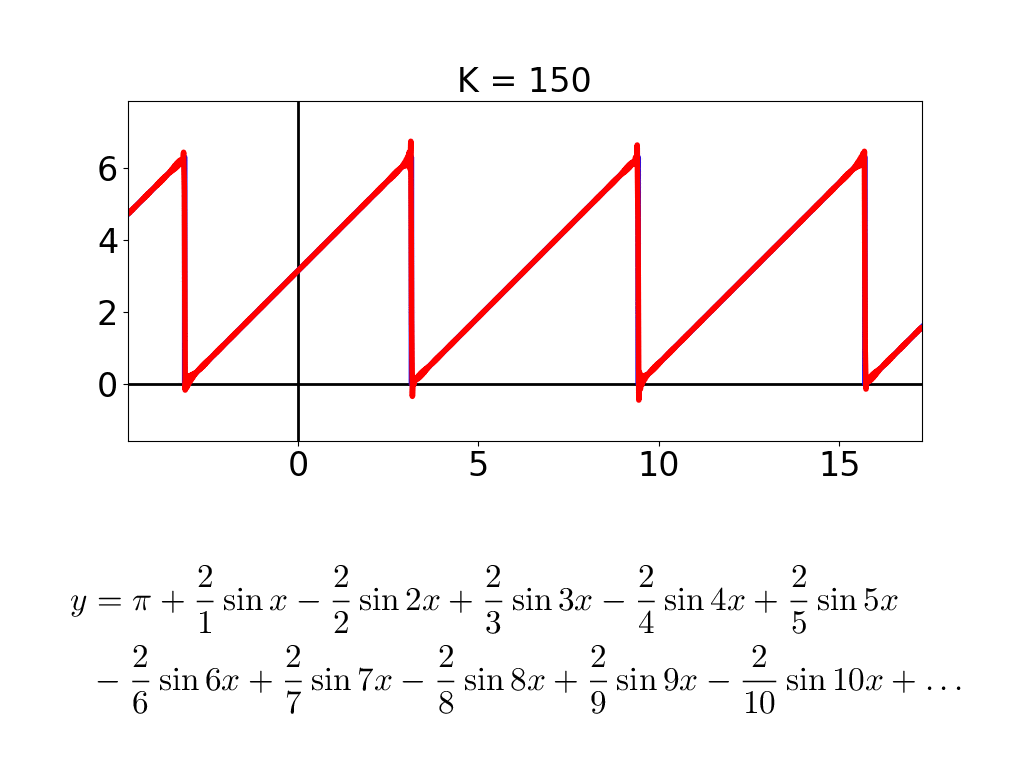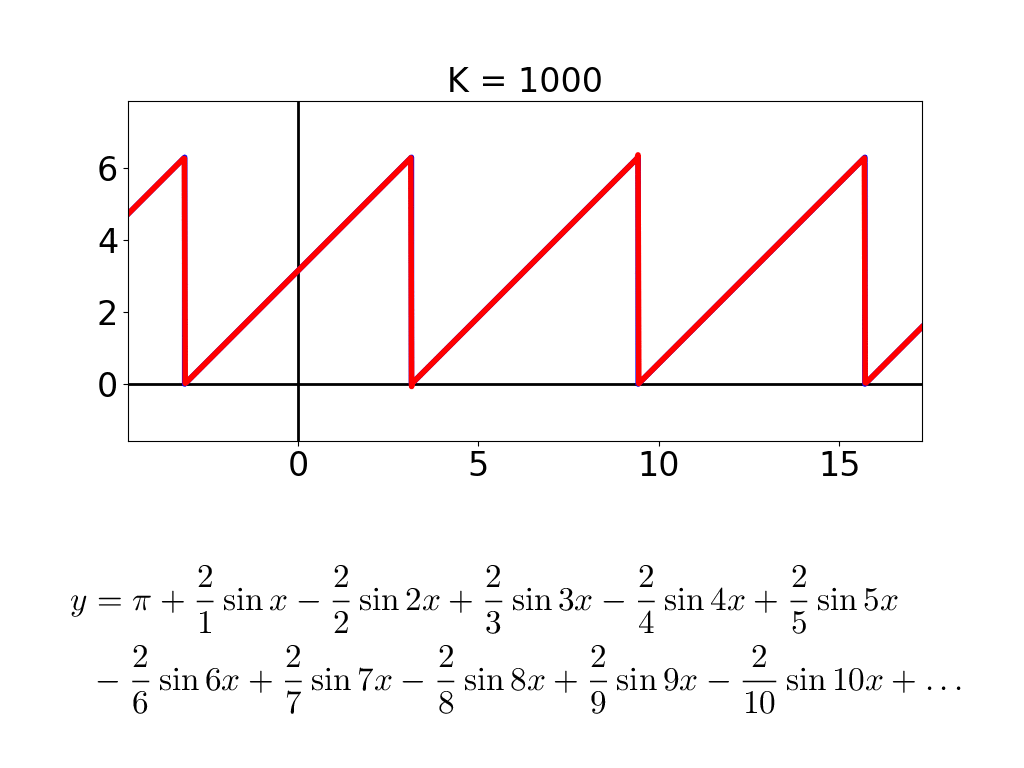
例えば，D = 1 のときはこんなん．
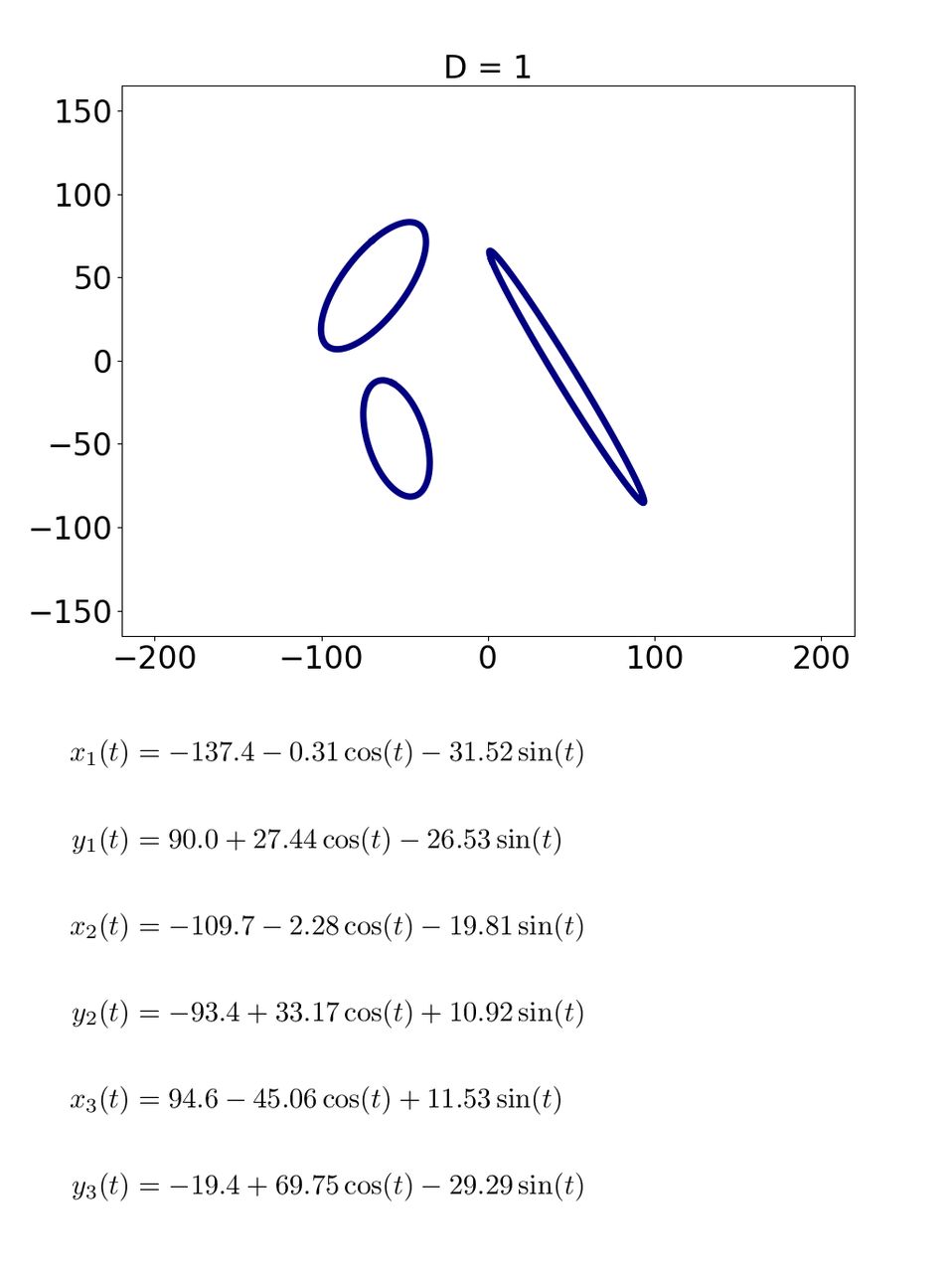
どの式も cos と sin が一つずつ入ってます．このとき図形は単純な楕円です．これが D = 2 になるとこーなります．
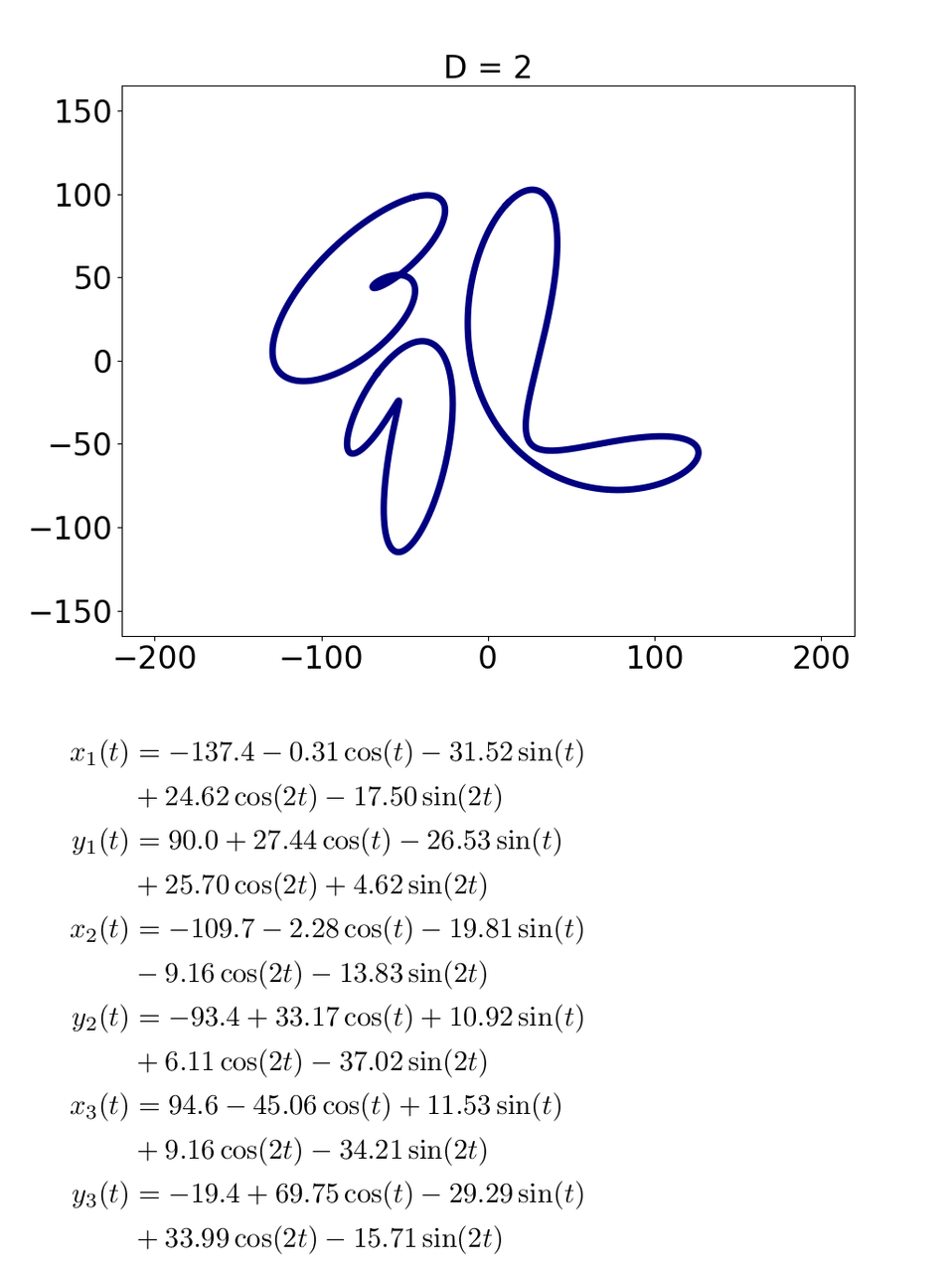
cos と sin が2つずつになって，形が少し複雑になりました．D = 20 まで行くと，cos, sin が20個ずつになって，こーなります．
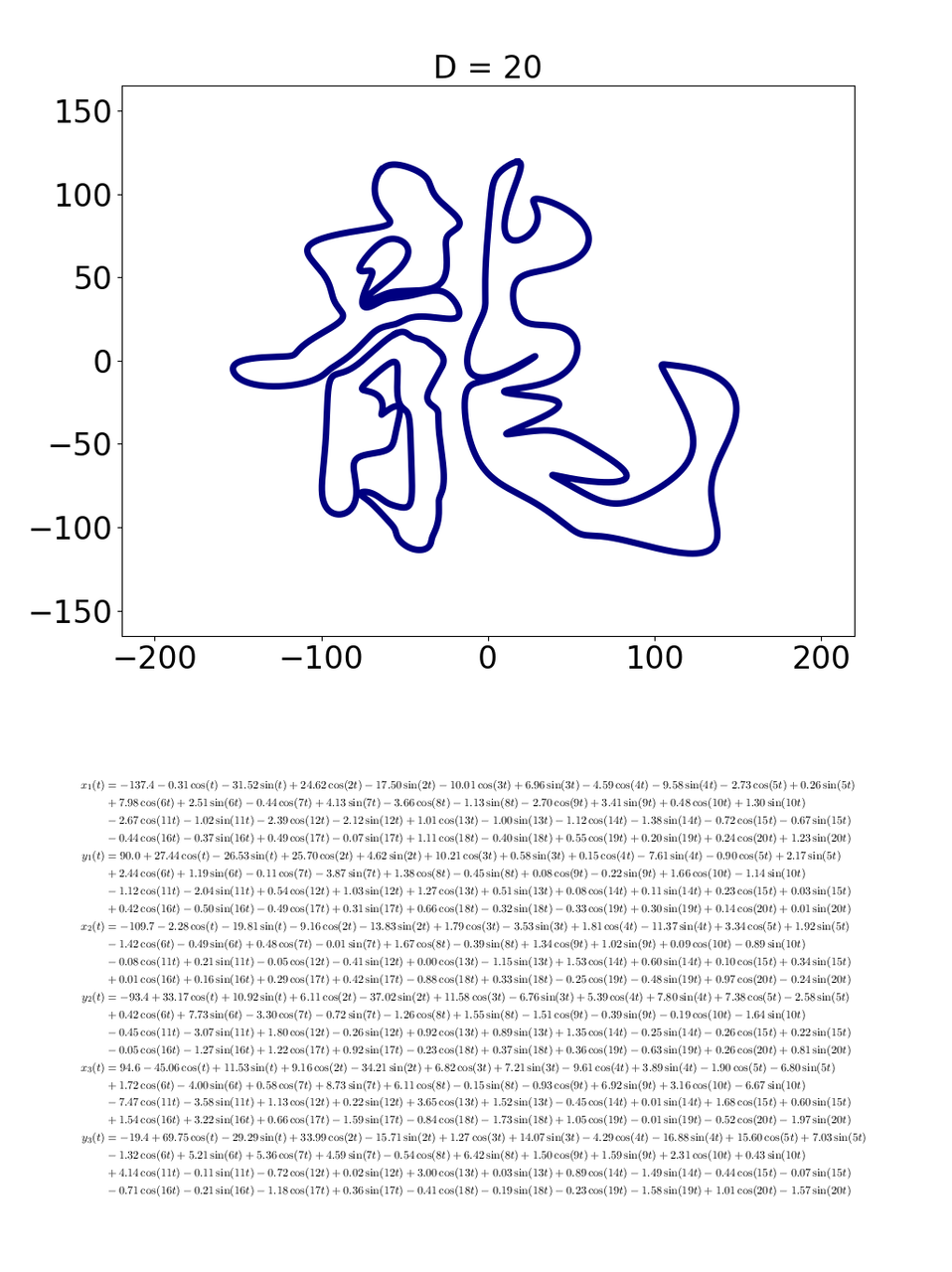
こんな調子で，式に出てくる cos と sin の数 D が増えると，描かれる図形がどんどん複雑になって，「龍」っぽくなっていきます．
この龍の字の場合，最初に上げた毛筆の画像をコンピュータで処理して
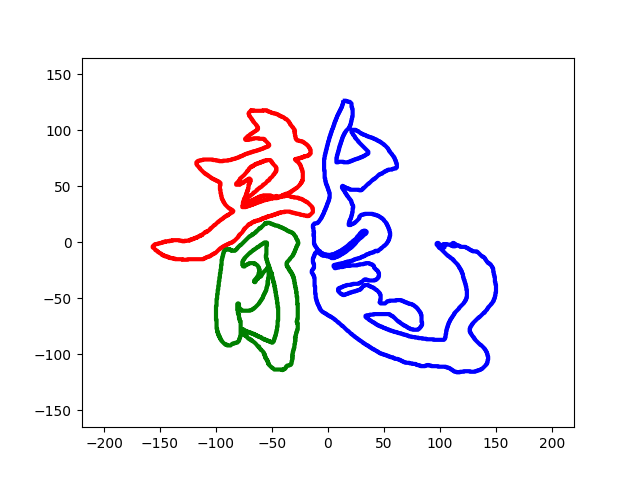
こんな風に輪郭線を見つけて，3つの輪郭線それぞれの座標を拾いました．それらをコンピュータに計算させて，各輪郭線を表す600個の sin, cos でできた式を求めました（さすがにこんなん手計算したくない (^^;）．その式を使って描いた曲線がこちら．
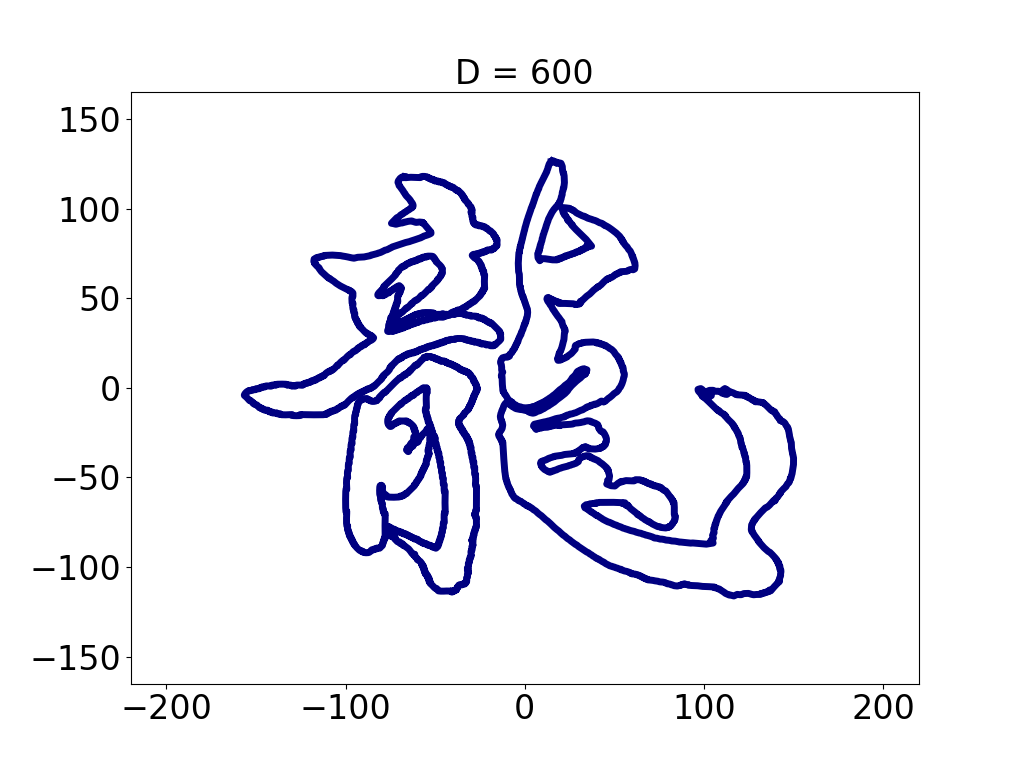
式の方はさすがに書く気になりませんので，省略します．なにしろ sin, cos が600個もある式やし．しかもそれが6つやし．上記の動画は，この600組の sin, cos でできた式を出発点にして，その中から sin, cos を1組だけ使う（D = 1） → 2組ずつ使う（D = 2） → ... → 600組全部使う（D = 600），ということをして作りました．
このように曲線を三角関数でできた式で表す方法は，フーリエ級数展開／フーリエ変換と呼ばれています．後で説明しますが，すごく応用範囲が広い（決してお絵描きのためだけのものではありません (^^; ）ので，大学で理工系へ進むとたいてい学ぶことになります．
ちう話のつづきは後でやることにしまして…．せっかくなので（？），得られた式を利用して遊んでみました．
（この動画は途中で止めてます．この場で完成するとこまでやるとお叱りを受けそ―なので (^^;）
龍と三角関数(2) - まんぼう日記 へつづく
2019年5月のてくてくメモ
（だいたい）2019年5月の週間歩行記録
| week | from | step(s) | step(a) | dist(s) | dist(a) | dist(t) |
|---|---|---|---|---|---|---|
| 18(268) | 0429 | 63997歩 | 9142歩 | 51.24km | 7.32km | 23251km |
| 19(269) | 0506 | 83851歩 | 11978歩 | 67.96km | 9.71km | 23319km |
| 20(270) | 0513 | 87461歩 | 12494歩 | 71.79km | 10.26km | 23391km |
| 21(271) | 0520 | 48351歩 | 6907歩 | 38.55km | 5.51km | 23429km |
| 22(272) | 0527 | 94112歩 | 13444歩 | 77.30km | 11.04km | 23506km |
s: 週合計，a: 週平均，t: 2014年第12週以降の累計
